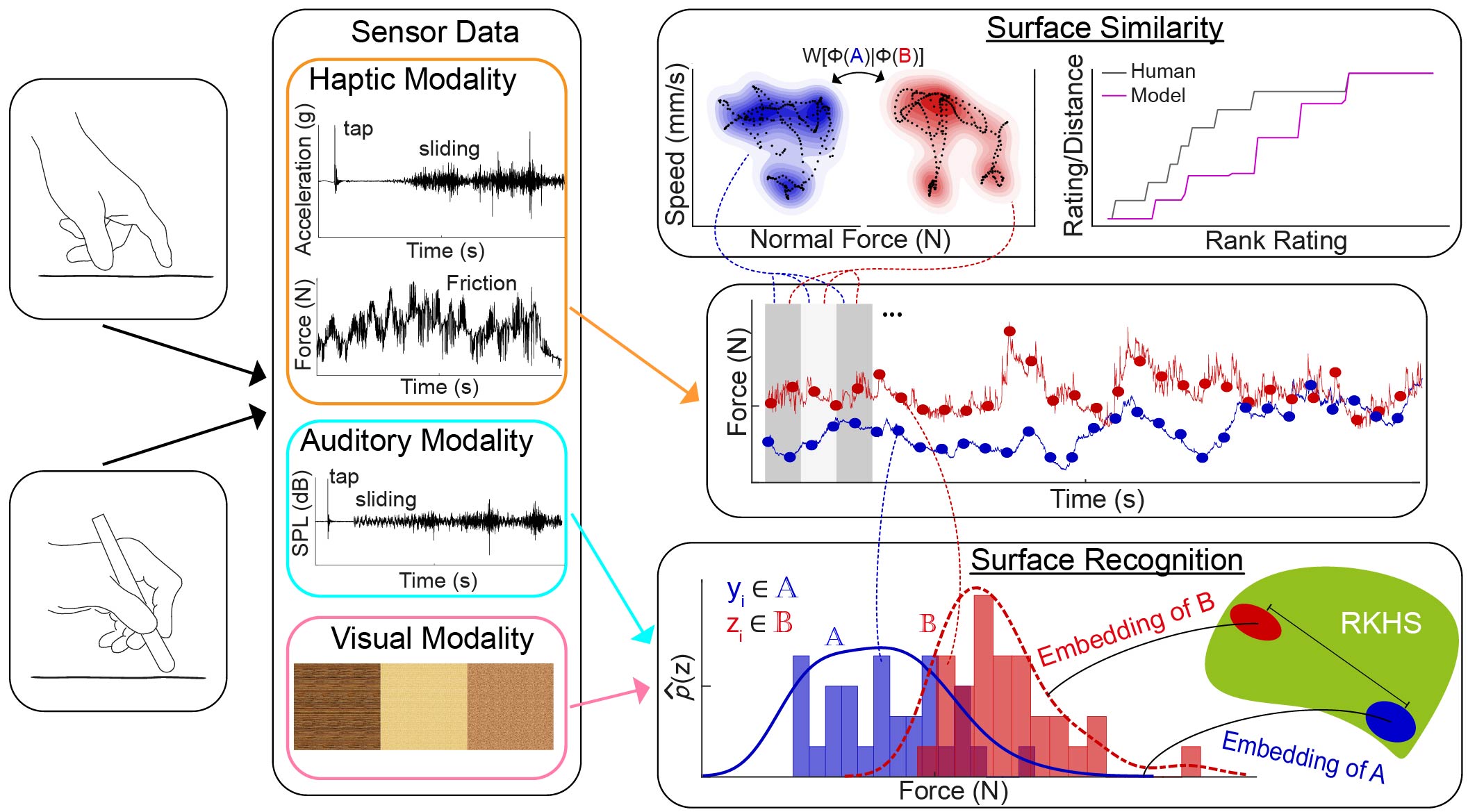
Sensor readings are recorded from finger-surface and tool-surface interactions. For surface similarity learning, the Wasserstein metric is used to compute distances between distributions of embedded features that are extracted from windows of interaction data. The embedding function is learned to match those distances to human similarity ratings. For surface classification, the kernel two-sample test is used to compare distributions of interaction data via kernel mean embedding.
When humans touch a surface with their bare finger or via a tool, they feel a rich array of haptic cues revealing its texture (e.g., friction and roughness) and material properties (e.g., deformability). Despite the rich information available from these interactions, research on surface perception and identification has generally either forgone interaction-specific analysis in favor of general surface descriptors or represented interactions as a large set of expertly crafted features taken over full interactions. In this research, we investigate how the physical data generated throughout entire interactions can represent surfaces in both perceptual and classification tasks.
We believe a natural way to consider full interactions is to analyze the underlying distributions of the contact-elicited signals, though such an approach has rarely been pursued before. We consider a variety of methods to represent these distributions and use probability distance metrics to compare interactions.
In our perceptual experiment, human subjects explore pairs of surfaces and rate the similarity of each pair while finger-surface interaction data are recorded [ ]. We partition the signals into overlapping windows and extract eight simple physical features (e.g., average force and vibration power) from each window. We learn a projection of the features into low-dimensional space such that the Wasserstein distances between pair-wise distributions match the perceived surface-pair dissimilarities.
For the surface classification task, a human drags a tool over a surface while various sensory information is captured (e.g., force and vibration) [ ]. By treating the interaction as a stochastic dynamical process, we can measure the underlying generative distributions of the surfaces by sparsely sampling over time or frequency.
We perform the kernel two-sample test on extracted samples with the maximum mean discrepancy (MMD) metric via kernel mean embedding.
As a result, we are able to classify a large number of surfaces in an automated fashion.
